Quanto è lunga una costa?
Svelato il mistero di un dato illogico
Come si sa, la scienza non ammette luoghi comuni né opinioni, perciò, quando diciamo che l’Italia ha 8.000, 8.500, 7.859 chilometri di coste, essa ci informa che stiamo dicendo una scempiaggine bella e buona. Incredibile ma vero. Ce lo spiega, appunto, uno scienziato.
Qualche tempo fa stavo seguendo il servizio di un telegiornale nel quale si parlava della Grecia e dell’incremento nella presenza degli italiani in quella terra meravigliosa. “Del resto – aggiungeva il giornalista di turno – si tratta del luogo ideale dove trascorrere le vacanze al mare poiché, oltre alla bellezza dei paesaggi, si dispone di un’ampia scelta: la Grecia ha infatti ben quindicimila chilometri di coste; molto più dell’Italia per la quale dobbiamo accontentarci di soli ottomila chilometri”.
Ecco, come fisico, sono meravigliato del fatto che in tv, sui giornali e persino su tanti libri ritenuti scientificamente rigorosi, come i testi di geografia o gli atlanti, venga indicato lo sviluppo costiero di un’intera nazione o anche solo di una piccola isola. Per esempio, ho letto che l’Italia avrebbe 7.859 chilometri di coste, mentre il perimetro di Ustica non raggiungerebbe i dodici.
Ebbene, vorrei dimostrarvi che questi dati numerici non hanno alcun senso, neppure approssimativamente. Sono pura fantasia e, pertanto, non ho neanche idea di quale criterio venga applicato per “inventarli”. No, mi correggo: qualche idea ce l’ho. Nel caso di un’isola, lo sviluppo viene forse valutato sommando le distanze tra i vari punti noti della costa (fari, tralicci, miragli eccetera) fino a completare il giro oppure misurando il percorso compiuto da un motoscafo che la circumnaviga a pochi metri di distanza da terra. Ma, se ci pensiamo un momento, queste valutazioni sono del tutto arbitrarie e, per di più, non hanno niente a che fare con la lunghezza della costa
Per capire come stanno le cose, ci basta semplicemente pensare a una piccola spiaggia che frequentiamo durante le nostre vacanze estive. Ebbene, guardando il mare, immaginiamo di voler valutare la lunghezza della costa che va da quello scoglio che vediamo laggiù, alla nostra sinistra, fino a quell’altro che si trova alla nostra destra. Cosa dobbiamo fare? Forse immaginiamo di tendere un lunghissimo metro a nastro, come quello utilizzato dalla Polizia Stradale per studiare la dinamica di un incidente?
Eh no. Facendo così troveremmo certamente la distanza tra quei due scogli ma non il valore che desideriamo ottenere. Già, perché per misurare la lunghezza di quel tratto di costa dobbiamo seguire minuziosamente le irregolarità della spiaggia. Questa infatti presenta piccole insenature così come, in altri punti, avanza verso il mare. Dobbiamo inoltre tenere conto del fatto che l’aspetto della battigia dipende dal livello della marea. Dobbiamo quindi stabilire se la lunghezza che abbiamo intenzione di misurare farà riferimento all’alta o alla bassa marea, o a una situazione intermedia. Ma ancora non basta. Ci troviamo, infatti, di fronte a un’altra circostanza importante: se il mare non è perfettamente fermo – e non lo è mai, ovviamente – l’aspetto della battigia muta continuamente, senza sosta. Come fare per individuare e quindi fissare una volta per tutte il confine tra terraferma e mare?
Possiamo pensare che la presenza di onde che modificano continuamente l’aspetto della spiaggia introduca soltanto un’imprecisione, una sorta di piccola indeterminazione nella misura che vogliamo ottenere. Meglio ancora, però, possiamo immaginare di essere fortunati e che il mare sia assolutamente calmo, così da permetterci di proseguire agevolmente nelle nostre misurazioni.
Allora, che cosa dobbiamo fare per tenere conto delle irregolarità della spiaggia? Per esempio, possiamo pensare di contrassegnare tanti punti lungo la battigia posandovi tanti sassolini, quindi misurare la distanza tra un sassolino e il successivo e infine fare la somma di tali distanze.
Con quale risultato? Troveremo un numero che è senz’altro maggiore rispetto a quello che avremmo ricavato tirando dritto tra i due scogli: infatti, una linea spezzata tra due punti è sicuramente più lunga della linea retta che li congiunge. Ma non ci possiamo fermare qui poiché la spiaggia presenta irregolarità anche tra un sassolino e l’altro. Dovremo dunque spezzettare anche questo piccolo tratto di battigia aggiungendo altri sassolini intermedi. In tal modo, la lunghezza di tutta la spiaggia risulterà ancora maggiore di quella calcolata in precedenza.
Cosa concludere? Per avere la “vera” lunghezza della spiaggia, dovremmo continuare con queste operazioni fino all’infinito, infittendo progressivamente la disposizione dei sassolini, trovando di volta in volta un numero crescente.
Ebbene, le considerazioni che abbiamo appena fatto ci portano a una sola conclusione: non è possibile definire la lunghezza di una costa. Neppure approssimativamente. E’ un calcolo impossibile proprio in linea di principio, non perché non siamo abbastanza abili per farlo. Questo si verifica poiché, come si dice in termini scientifici, la battigia presenta una struttura frattale, per la quale il concetto stesso di lunghezza perde senso. La parola “frattale” è un neologismo coniato dal matematico di origine polacca Benoît Mandelbrot (1924-2010) per denotare proprio la frazionabilità infinita che caratterizza questo genere di strutture.
Non siete ancora convinti? Vi proporrò allora alcune considerazioni che potranno aiutarvi a capire che, invece, le cose stanno proprio così.
Se ci chiediamo quanto è lunga l’autostrada A1 che ci porta da Roma a Milano, possiamo rispondere che si tratta di circa cinquecento chilometri. Possiamo accontentarci di questa valutazione approssimativa oppure essere più precisi. In ogni caso la risposta ha sicuramente un senso logico.
Ma immaginiamo ora di chiederci quanto è lungo, sempre da Roma a Milano, il confine tra il lastricato dell’autostrada – quello asfaltato – e la terra incolta che si trova ai suoi margini. Sempre cinquecento chilometri, chilometro più chilometro meno? Eh no! Pensando anche a un solo metro di autostrada, ci accorgiamo che dovremmo seguire l’andamento di tutti i piccoli granuli di asfalto che si trovano sul margine.
Dovremmo fare un po’ come quella formica che stiamo osservando mentre trasporta una piccola mollica di pane, facendo il percorso a zig zag lungo quel breve tratto. Quanto avrà camminato per percorrere quel metro di autostrada lungo il bordo? Chissà, forse più di dieci metri!
Sono davvero tante le volte nelle quali mi è capitato di esporre questi argomenti e, in più di un’occasione, mi è toccato quasi litigare nella speranza (molto spesso vana) di convincere chi mi ascoltava. Una volta, in particolare, dopo questo discorso sulla lunghezza delle coste, mi è stato chiesto: ma allora, anche quando leggo che Ustica si estende per poco più di otto chilometri quadrati, devo considerare questo dato privo di senso, come quello che fissa il suo sviluppo costiero in circa dodici chilometri? Domanda più che lecita, ma stavolta la risposta è diversa: se quello della lunghezza della costa è un dato assolutamente privo di senso, quello dell’estensione superficiale ne ha invece uno ben preciso e lo possiamo ottenere con una certa approssimazione che, peraltro, possiamo progressivamente migliorare.
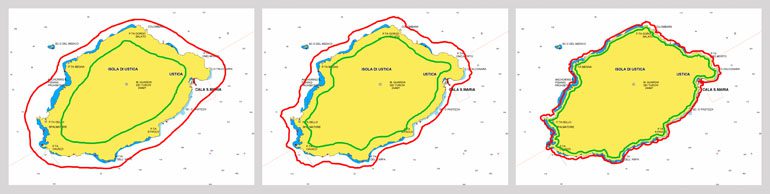
Vediamo perché. Prendiamo la carta nautica e, con una matita rossa, tracciamo una linea chiusa che contiene al suo interno tutta Ustica. Poi, con una matita verde, tracciamo una seconda linea chiusa, stavolta su tutta la terraferma, in prossimità della costa.
 Utilizzando un planimetro, possiamo misurare sulla carta l’area delle due superfici racchiuse rispettivamente dalla linea rossa e da quella verde. Evidentemente, la prima risulterà maggiore della seconda. Quindi potremo dire che, sul disegno, la superficie di Ustica corrisponde a un valore compreso tra quelli delle due aree, per esempio definendolo come media aritmetica. Basterà fare una proporzione con la scala della carta nautica per ottenere il valore della superficie nella realtà.
Utilizzando un planimetro, possiamo misurare sulla carta l’area delle due superfici racchiuse rispettivamente dalla linea rossa e da quella verde. Evidentemente, la prima risulterà maggiore della seconda. Quindi potremo dire che, sul disegno, la superficie di Ustica corrisponde a un valore compreso tra quelli delle due aree, per esempio definendolo come media aritmetica. Basterà fare una proporzione con la scala della carta nautica per ottenere il valore della superficie nella realtà.
Se il risultato ci sembra troppo approssimativo, possiamo ripetere la stessa procedura disegnando però le due curve chiuse – sempre una all’esterno e una all’interno della costa – in modo un po’ più preciso rispetto alla forma dell’isola e quindi ravvicinandole: la differenza tra le aree delle due superfici risulterà più piccola e, in questo modo, potremo definire il valore della superficie dell’isola con maggiore precisione. Se ancora non ci bastasse, possiamo ripetere più volte l’operazione, ogni volta perfezionando il disegno delle due linee e, quindi, ottenendo un dato sempre più preciso.
Come si può notare, è esattamente il contrario di quel che abbiamo osservato a proposito della misura delle coste.